The 2002 and 2007 reports of the National Assessment of Educational Progress (NAEP) writing as ses sment (National Center for Education Statistics, 2008), administered to 8th and 12th graders, show an increase in writing scores. Applebee and Langer’s (2006) analysis of NAEP data as well as other sources published during the decade preceding their review revealed that the more frequently students reported writing one or more paragraphs in science and social studies, the higher their writing achievement.
The results, however, were lower in mathematics. “It may be that at the classroom level, the role of writing in mathematics instruction has not been well conceptualized” (Applebee & Langer, 2006, p. 14). Indeed, many teachers find it more natural to integrate writing and science (e.g., Varelas, Pappas, Kokkino, & Ortiz, 2008) or writing and social studies (e.g., Jones & Thomas, 2006). Wolsey (2010) examined the complexity of student writing and vocabulary learning in a cross-disciplinary writing project involving English, science, and social studies. Where was mathematics?
That we see so few examples of the integration of writing and mathematics in educational literature seems surprising, considering that the mathematics education community has affirmed the importance of such integration for many years. As early as 1989, the National Council of Teachers of Mathematics (NCTM) identified learning to communicate mathematically as a major goal for students.
In 1992, Countryman’s book, Writing to Learn Mathematics: Strategies That Work, K-12, captured the attention of mathematics educators amid a flurry of interest and ideas (e.g., Quinn & Wilson, 1997; Sipka, 1990). Almost a decade later, NCTM (2000) specifically stressed writing as “an essential part of mathematics and mathematics education” (p. 60) in the landmark document Principles and Standards for School Mathematics.
Still, many teachers struggle to link writing and mathematics and honor the integrity of both disciplines at the same time. Teachers of writing might say that if students are assigned to describe the process they used in solving a problem with no revision or editing, the quality of integration is drawn into question. Teachers of mathematics might say that if students are asked to write a report on a famous mathematician they may not be engaged in developing mathematical reasoning no matter how many drafts they write. Although the appropriate balance may be elusive, the endeavor is nevertheless worthy of being undertaken (e.g., Applebee, 1984; Bossé & Faulconer, 2008; Newell, 2008).
There are two levels of integration that teachers may use as a beginning point. Writing without revision, the first level, can be readily worked into mathematics instruction. Writing with revision, the second level, may take more time but enables teachers to connect the writing process more fully with mathematics instruction. Each level can be appropriate under differing circumstances.
In Carter’s (2009) description of writing tasks in her mathematics instruction, both levels are reflected. She had her students write in what she called “mathematical notebooks” (p. 607), which required little or no revision. She also had her students write about mathematics in a process-oriented way during writing workshop. Some wrote stories such as “The Hexagon Adventure” and “The Magical Subtracting Frying Pan.” Others wrote autobiographies such as “How I Learned to Do Math in Kindergarten and Beyond.”
Although Carter’s (2009) reflective mathematical journals and stories about mathematical concepts in writing workshop may not represent an ideal solution, they demonstrate one teacher’s exploration of the possibilities. This article presents six additional examples, including student work, in which teachers have attended to the goals of both writing and mathematics. By no means are these ideas new. Teachers may have been introduced to them before, but perhaps not in the context of mathematics. Although the following suggestions are not exhaustive, teachers have found them to be a promising place to begin.
Writing without revision
Learning logs
As students start class, they are given a prompt to which they respond for a few minutes in writing. The task is not designed as a mathematics problem per se, but rather to encourage students to focus on mathematics.
One fifth-grade teacher typically used learning logs to review previously learned material. On one occasion, the prompt she posed was, What did we learn about mean, median, and mode? Most students wrote at least a half page filled with definitions and examples (see Figure 1A). While studying probability, one student wrote the following definition: “The ‘probability’ of something is how likly your gonna get, pick, or find something.” He then gave an example using shapes and colored cards (see Figure 1B).
Figure 1A: Learning log entries by fifth graders — definitions and examples of mean, median, and mode

Figure 1B: Learning log entries by fifth graders — definition and examples of probability

This teacher found that the quality of the learning logs improved as students shared their work: “[When a student shared] a log that showed clear understanding, this provided others with an example to follow.” Along with finding learning logs to be an effective way to introduce or close a lesson, the teacher observed that the quality of student discussion of mathematics during lessons was richer when students were expected to write.
Learning logs honor the integrity of writing when students write their own connections and examples. At the same time, they foster mathematical understanding by engaging the minds of students in transforming information from facts to be memorized to the construction of meaning (e.g., Newell, 2008).
Think-write-share
Teachers often ask questions and count on having at least one or two students raise their hands. One 2011fourth-grade teacher tried to involve everyone in the class by allowing think time and expecting students to write before sharing. For one think-write-share, she asked, “What is an equivalent fraction?” She gave the students a few minutes to think and then asked them to write their responses before calling on students to share, using a document camera. In reflecting on the use of this strategy, the teacher commented,
I assumed that everyone understood [what an equivalent fraction is], because we’ve done it for a while. However, as we shared, I soon realized that some of my students thought that equivalent fractions were [only] fractions that were the same, for example, 1⁄4 = 1⁄4.
To address this misconception, the teacher strategically selected students to share based on the thinking she had seen demonstrated: “Kids who were getting it wrong, kids who were getting it a little, and those who knew it well.” Once several clear responses had been shared and discussed (see Figure 2A), the teacher invited all students to write again, revising their original work to reflect their increased understanding (see Figure 2B).
Figure 2A: Think-write-shares by fourth graders — example showing a clear understanding of equivalent fractions
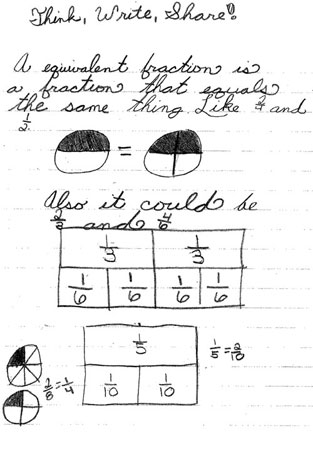
Figure 2B: Think-write-shares by fourth graders — example of equivalent fractions, before and after revision

The think-write-share strategy heightens student engagement in writing. Concurrently, students are held accountable for their own mathematical understanding.
Note-taking/note-making
Students may be accustomed to taking notes, but now ask them to make notes as well. Along with listing the main points of a lesson, students can write their own reflections and perceptions. One fifth-grade teacher used the strategy of note-taking/note-making in mathematics to extend the notion of whole numbers to integers, including the concept of negative number.
She asked her students to fold their papers in half vertically. On the left side, she directed students to define integers and construct number lines to demonstrate relative size of integer pairs. On the right side, students wrote their own reactions and observations. One student wrote, “I will remember that on the negitive side the bigger it gets the smaller it is. I thought that was cool.” Another student wrote, “It is weird that -2 is greater than -5.” This same student went on to create his own analogy: “It is like a piano, lower to higher with middle C. Smaller to larger with zero. Zero and C aren’t small, big, high, or low” (see Figure 3).
Figure 3: Note-taking/Note-making: A fifth grader’s conception of integers

Note-taking/note-making honors both writing and mathematics. It encourages students to make connections between new concepts and previously learned material and their personal experiences.
Writing with revision
Shared writing
A third-grade teacher used shared writing with her students to review what they had learned in their geometry unit. Using chart paper, the teacher recorded a student-generated word bank that included face, edge, vertex, congruent figures, and polygons. On subsequent sheets, the teacher used a black pen to record in sentences what the students shared about their learning. Next she guided them to suggest revisions and additions to their shared writing and recorded those suggestions with a different colored pen.
Some changes related to word choice (“learning about geometry” became “learning and exploring geometry”), while other changes related to geometry concepts. In the shared writing, students had listed 3-D shapes such as spheres, cones, cubes, and cylinders and had given real-life examples. During revision, students added the following sentence that went beyond visualization to include attributes: “Some 3-D figures will have vertexes (corners), edges, and faces.” Students then suggested three titles and voted on which title was best (see Figure 4).
Figure 4: A shared writing about geometry composed and revised by third graders and their teacher

This teacher valued shared writing as an engaging strategy to help students internalize mathematics:
I feel that this experience has helped them go beyond recording the information in their math journals and just doing our assignments…. I think it helped to make it more personal and [validate] what was important to them.
As students engaged in revising, they improved the writing while extending their mathematical thinking (see Whitin & Whitin, 2000). Because the mathematical ideas are constructed through group interaction, students help one another learn to communicate mathematically.
Class book
Using a similar process, a teacher can make a class book with students. Once a shared writing is completed on chart paper, the teacher numbers the sentences and assigns each student a numbered part to write as a final draft for a page in the class book. Very little time is required for the teacher to move from student to student and edit sentences. As the teacher edits, students are encouraged to create representations for the idea on their page.
When the students are finished, the teacher gathers the pages in order and adds a cover with a title. When the shared writing has only a few sentences, the teacher assigns several students the same number and creates several covers. In this way, students produce multiple copies of the same book. One could be kept in the classroom and others given to teachers of younger grades for their reading centers.
A fourth-grade teacher used a variation of this strategy with her students. This teacher’s prompt was to create and illustrate a word problem using fractional parts of a set of 24 (see Figure 5). Every student’s work became a page in the class book.
Figure 5: A class book page about word problems written and illustrated by fourth graders

Class books provide a sense of audience as well as an opportunity for students to revise and edit their writing. Simultaneously, the format invites students to “create and use representations to organize, record, and communicate mathematical ideas” (NCTM, 2000, p. 67).
Alphabet books
One fifth-grade teacher helped her students create alphabet books to develop mathematics vocabulary. She assigned students letters of the alphabet and sent them on a search for new and complex words in their mathematics textbook, notes, thesaurus, and mathematics dictionary (e.g., Monroe, 2006). Students were assigned to use each word in a meaningful sentence, draw an appropriate representation, or write a real-world connection (see Figure 6). The teacher explained,
Because the format of an alphabet book requires brevity, I can readily respond to what students have written individually in short conferences, offering both compliments and suggestions for improvement. I can discuss their mathematical thinking and their writing in the same conference.
Figure 6: A class book page about word problems written and illustrated by fourth graders

Students then revise and edit as they prepare a final draft for publication. This teacher prefers to have the book professionally printed, using an inexpensive online publishing tool (e.g., mightyauthors.com).
Alphabet books not only introduce students to a delightful genre, but also allow students to experience every phase of the writing process. At the same time, they honor the integrity of mathematics by helping students develop vocabulary essential for mathematical thinking. The format invites the use of meaningful communication through words, graphic representations, and symbols.
A call for additional strategies
These six ideas represent only a place to begin. Creative teachers will use these ideas as springboards to additional strategies for integrating their writing and mathematics instruction. Numerous and varied opportunities for this integration support students as they learn to think their way into mathematics and make it their own (Zinsser, 1988) and also become more aware of the range of writing possibilities available to them (Newell, 2008). Such opportunities are not superfluous or simply nice to do if there is enough time. They are too important to ignore.
Wilcox, B. and Monroe, E. E. (2011), Integrating Writing and Mathematics. The Reading Teacher, 64: 521-529. doi: 10.1598/RT.64.7.6
